Helper Functions
In class we discussed in addition to the stereotypical recursive
patterns in the book, the ``helper function with something extra''
pattern. This is a page of notes about that.
Reverse
Let's say we want to define a function rev that takes a
sentence and returns that sentence with the words in reverse order.
For example:
(rev '(aye bee sea)) ; (sea bee aye)
(rev '(ex)) ; (ex)
(rev '()) ; ()
-
Earlier we learned a cute but tricky way to do this using higher order
functions:
(define (rev sen)
(accumulate (lambda (x y) (sentence y x))
sen))
but let's say we want to do it recursively.
-
A straightforward thought is to take the reverse of the sentence
with it's first element removed, and then put that first element on at
the end.
(define (rev sen)
(if (empty? sen)
'()
(sentence (rev (butfirst sen)) (first sen))))
Let's look at a call graph for (rev '(a b c d)), to make sure
we understand how it works.
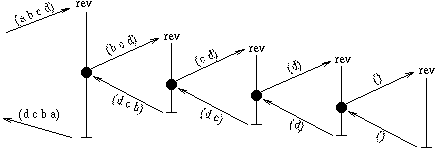
That's nice, but maybe inefficient, because it is expensive to tack
things onto the end of a sentence but cheap to tack them onto the
beginning.
-
We can use a ``helper function with something extra'' instead. The
helper function will take two arguments: a sentence to go at the end
of its result, and a sentence to be reversed and put at the
beginning. For example:
(rev-aux '(aye bee sea) '(one two three)) ; (three two one aye bee sea)
So let's define it:
(define (rev sen)
(rev-aux '() sen))
(define (rev-aux end-of-result to-be-reversed)
(if (empty? to-be-reversed)
end-of-result
(rev-aux (sentence (first to-be-reversed)
end-of-result)
(butfirst to-be-reversed))))
This should be efficient because it only moneys around with the
beginning of sentences.
Let's look at a call graph of (rev '(a b c d)), to see if we
can understand this.
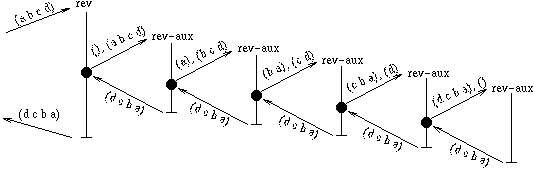
Parallel Prefix
Consider the function pp+, which is supposed to compute the
``parallel prefix'' of a sentence of numbers. That is, a sentence of
the running totals.
For example:
(pp+ '(1 1 1 1 1)) ; (1 2 3 4 5)
(pp+ '(1000 200 30 4)) ; (1000 1200 1230 1234)
(pp+ '(14)) ; (14)
(pp+ '()) ; ()
As with most problems, there are a bunch of different strategies we
might use here.
- Simple recursion: cut off the first elt, figure out the parallel
prefix of the rest, and modify it to give the right answer.
(define (pp+ sen)
(if (empty? sen)
'()
(let ((fir (first sen)))
(sentence fir
(every (lambda (x) (+ x fir))
(pp+ (butfirst sen)))))))
This looks nice, except one might worry about efficiency, in that
shared partial sums are not being used, so it might take too much time
to compute.
-
Instead we can try to do it from the other direction, recursing by
removing the last element:
(define (pp+ sen)
(if (empty? sen)
'()
(let ((partial-pre (pp+ (butlast sen))))
(sentence partial-pre
(+ (last sen)
(if (empty? partial-pre)
0
(last partial-pre)))))))
This seems elegant, in that it uses the already-computed total for the
first part of the sentence in calculating the remaining numbers, so it
will not do too many additions. But it might be inefficient for a
different reason: first is fast, while last takes
time of order the length of the sentence, as does tacking a new
element onto the end of a sentence.
-
In an attempt to have our cake and eat it too, we can define
pp+ in term of a recursive helper function, which takes an
extra argument: the running total so far.
(define (pp+ sen) (pp+-aux 0 sen))
(define (pp+-aux running-total sen)
(if (empty? sen)
'()
(let ((new-running-total (+ running-total (first sen))))
(sentence new-running-total
(pp+-aux new-running-total
(butfirst sen))))))
Which is efficient both in its manipulation of the sentence and in
taking advantage of the left-to-right structure of the addition.
Let's look at it's call graph for (pp+ '(1000 200 30 4))
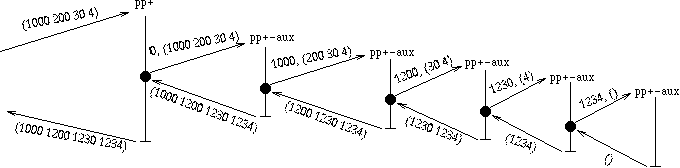
The Fibonacci Sequence
Another problem we can use helper functions for is the Fibonacci
function discussed in the text. (We all know where the Fibonacci
sequence comes from: it's the number of female rabbits you have each
year, if you buy a female rabbit the first year, each litter contains
one female rabbit, there is one litter a year, rabbits live for two
years, and there is no shortage of male rabbits. The Fibonacci
sequence also comes up in spiral growth patterns, like the whorls in a
sunflower.)
Each element in the sequence is the sum of the previous two elements:
1, 1, 2, 3, 5, 8, 13, 21, 34, etc.
We want to define our function such that
(fibb 0) ; 1
(fibb 1) ; 1
(fibb 2) ; 2
(fibb 3) ; 3
(fibb 4) ; 5
(fibb 5) ; 8
(fibb 6) ; 13
(fibb 7) ; 21
(fibb 8) ; 34
The obvious recursive definition is:
(define (fibb n)
(cond ((= n 0) 1)
((= n 1) 1)
(else (+ (fibb (- n 1)) (fibb (- n 2))))))
This will be very inefficient for large arguments: the total
number of recursive calls is going up exponentially with the argument!
We can see that by sketching the call graph of (fibb 8)
 If you think about it, you'll see that the function either recurses
with two calls to itself or returns 1. So the total number of calls
to fibb when you go (fibb n) must be twice the
returned result minus one. This grows pretty quickly.
If you think about it, you'll see that the function either recurses
with two calls to itself or returns 1. So the total number of calls
to fibb when you go (fibb n) must be twice the
returned result minus one. This grows pretty quickly.
Instead we would like to sum things up as we would if we were doing
this by hand. Doing it by hand, we would keep track of the previous
two Fibonacci numbers to calculate the next one, and repeat that until
we get up to where we want to be.
This can be done with a helper function that takes three arguments:
the last two Fibonacci numbers, and the number of steps that remain to
be taken.
(define (fibb n)
(fibb-aux 1 1 (- n 1)))
(define (fibb-aux fibb-nm1 fibb-n steps-remaining)
(cond ((= steps-remaining 0) fibb-n)
((= steps-remaining -1) fibb-nm1)
(else (fibb-aux fibb-n
(+ fibb-nm1 fibb-n)
(- steps-remaining 1)))))
This gives a much faster algorithm, as seen from the following call
graph for (fibb 8)
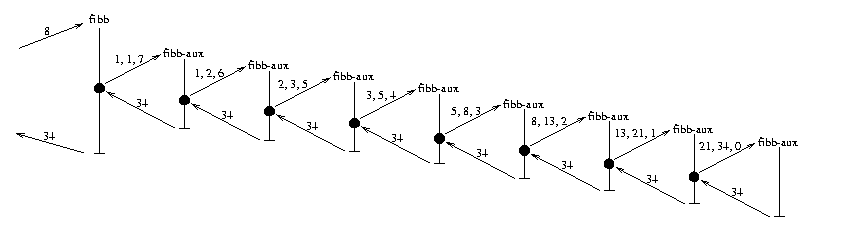
Barak Pearlmutter <bap@cs.unm.edu>


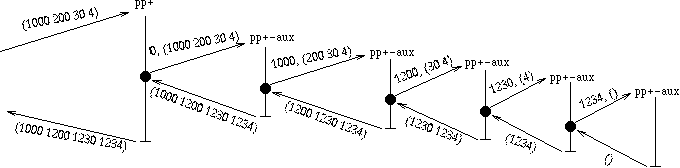
 If you think about it, you'll see that the function either recurses
with two calls to itself or returns 1. So the total number of calls
to fibb when you go (fibb n) must be twice the
returned result minus one. This grows pretty quickly.
If you think about it, you'll see that the function either recurses
with two calls to itself or returns 1. So the total number of calls
to fibb when you go (fibb n) must be twice the
returned result minus one. This grows pretty quickly.
