Name ___________________________________
Final Exam, ECE 547 Fall 1998
This exam is take-home and open book, but obviously it is to be done
individually and not in teams, and you should not discuss the problems
with anyone else. It is due (either by email or physical paper) by
5pm Thursday December 17.
Answer eight of the following nine questions (12.5 points each.)
- What is the difference between Rosenblatt's Perceptron
Learning Rule and backpropagation applied to a single
linearity-followed-by-a-sigmoid unit? (Briefly, please!)
- What are the disadvantages (and symptoms) of using too many hidden
units when trying to train a network using a fixed training set? What
are the disadvantages (and symptoms) of using too few?
- If your error measure is the Kulback-Liebler divergence, and the
target distribution (over just four possibilities) is p=(0.1 0.1 0.4
0.4), which would have lower error, q1=(0.001 0.001 0.499 0.499) or
q2=(0.25 0.25 0.25 0.25)?
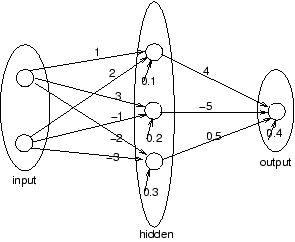
- Calculate the gradient dE/dw=(dE/dw1 dE/dw2 ...) of the ``vanilla
backpropation network'' shown below, with a single input pattern (0.7
0) and a target output of 0.9. The extra incoming arrow are for
biases. Show all intermediate calculations.
- What good are hidden units? Why don't support vector machines
need them?
- What does the Q in Q-learning stand for? What advantages does
Q-learning have over just estimating V(state), the value of individual
states? (Hint: off-policy.)
- When a Boltzmann Machine learns, what is it trying to do?
- Boltzmann Machines use stochastic binary units. Why?
- Describe three methods for helping networks generalize better.
For each give an example of where it might be appropriate.
Barak Pearlmutter
<bap@cs.unm.edu>

