 The text of a computer program sits in a text file, frozen and
lifeless. Then by some magical process, this inanimate text has life
breathed into it!
The text of a computer program sits in a text file, frozen and
lifeless. Then by some magical process, this inanimate text has life
breathed into it!
LISP is a ball of mud.
- Alan J. Perlis
 The text of a computer program sits in a text file, frozen and
lifeless. Then by some magical process, this inanimate text has life
breathed into it!
The text of a computer program sits in a text file, frozen and
lifeless. Then by some magical process, this inanimate text has life
breathed into it!
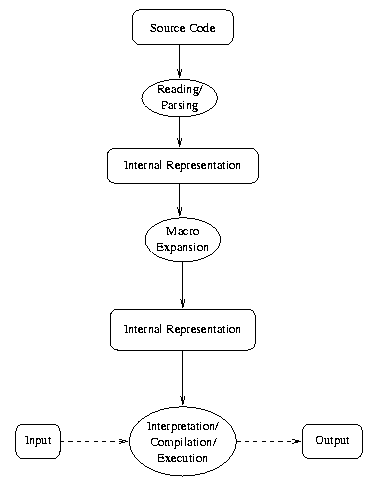
This animation proceeds though a few stages.
(define (my-load filename)
(eval-no-macros (macro-expand (read-sexpr-from-file filename))
'()))
(define (macro-expand expr)
(if (not (pair? expr))
expr
(let ((keyword (car expr)))
(cond ((equal? keyword 'QUOTE) expr)
((equal? keyword 'LAMBDA)
(list 'LAMBDA
(cadr expr)
(macro-expand (caddr expr))))
(else
(let ((expander (get-macro-expander keyword)))
(if expander
(macro-expand (expander expr))
(map macro-expand expr))))))))
(define (eval-no-macros expr env)
(cond ((symbol? expr) (lookup expr env))
((pair? expr)
(cond ((equal? (car expr) 'QUOTE) (cadr expr))
((equal? (car expr) 'LAMBDA) (make-lambda expr env))
(else
(let ((lis (map (lambda (x) (eval-no-macros x env))
expr)))
(my-apply (car lis) (cdr lis))))))
(else expr)))
If we wanted to avoid the work of expanding macros in parts of the
code that are never actually run (but run the risk of not noticing
poorly formed macros in such code, and expanding macros in lambda
bodies many times) we can integrate these two processes:
(define (my-load filename)
(my-eval (read-sexpr-from-file filename) '()))
(define (my-eval expr env)
(cond ((symbol? expr) (lookup expr env))
((pair? expr)
(let ((keyword (car expr)))
(cond ((equal? keyword 'QUOTE) (cadr expr))
((equal? keyword 'LAMBDA) (make-lambda expr env))
(else
(let ((expander (get-macro-expander keyword)))
(if expander
(my-eval (expander expr) env)
(let ((lis (map (lambda (x) (eval-no-macros x env))
expr)))
(my-apply (car lis) (cdr lis)))))))))
(else expr)))
STk integrates macro expansion with evaluation of the core language,
but serious Scheme implementations (T, mzscheme, rscheme, chez scheme,
oaklisp, scheme48, etc) keep the two stages distinct. In fact, really
serious scheme implementations don't have an interpreter of the sort
described above at all, but implement the eval-no-macros part
by compiling everything to machine code.
We were above in the fortunate situation of implementing Scheme in Scheme. This meant that the language in which we wrote our macro expanders was itself Scheme. However, it is not always the case that the macro expanders are written in the target language. For instance, in C macros are defined in a very weak language called cpp.
#define DO0(i,n) for ((i)=0; (i)<(n); (i)++)
main()
{
int j;
DO0(j,21) {
printf("%d %d", j, j*j)
}
}
In general, if you really need to use macros, and the native macro-expansion system of the language you are writing in is insufficient for your needs, you can use some other macro-expansion language. A particularly popular example of this is the m4 macro language, which is used as a preprocessing step by many language interpreters. There is no reason you can't use it with, eg, C++.
However, even the more powerful m4 is unable to implement the symbolic differentiation macro discussed below.
In general, macros can be used for two things:
(define (foo n)
(if (= n 0)
0
(+ (sqr n) (foo (- n 1)))))
(define (sqr x)
(* x x))
This works fine, but let's say we want it to be faster because it's in
the time-critical inner loop of some program we're writing. Okay, we
could do a number of things: we could change it to make the loop
tail-recursive, we could sit at a blackboard and realize there's a
closed-form solution (/ n (+ n 1) 2). But imagine we're not
thoughtful enough to look for a simpler solution, and that our
profiling tools have shown us that most of the time in the program is
spent calling the sqr routine.
We can ``manually inline'' the code for sqr, leading to
(define (foo n)
(if (= n 0)
0
(+ (* n n) (foo (- n 1)))))
but imagine that the function in question were a little more
complicated, and that it might need to be changed.
If our implementation was good, it might automatically inline the sqr routine during compilation, or there would be some way to ask it to inline the call. But say our implementation was deficient in this regard. We could then resort to a macro:
(define sqr
(macro expr
`(let ((s ,(cadr expr)))
(* s s))))
This is an example of using a macro to compensate for a deficiency of
the implementation: an inability to properly inline procedures
combined with very slow procedure calls.
In general this should be a last resort, to be used only when all other measures have proven inadequate.
(let ((key (foo x))) (cond ((or (equal? key 'one) (equal? key 'uno)) 1) ((or (equal? key 'two) (equal? key 'dos)) 2) ((or (equal? key 'three) (equal? key 'tres)) 3) ((or (equal? key 'four) (equal? key 'quatro)) 4)))more readably, by defining a switch macro so that
(switch (foo x) ((one uno) 1) ((two dos) 2) ((three tres) 3) ((four quatro) 4))expanded to the more above cond. We can accomplish this by defining a macro expander
(define (macro-expand-switch expr)
`(let ((key ,(cadr expr)))
(cond ,@(map (lambda (clause) (expand-switch-clause 'key clause))
(cddr expr)))))
(define (expand-switch-clause key-var clause)
`((or ,@(map (lambda (k) `(equal? ,key-var ',k))
(car clause)))
,(cadr clause)))
;;; this plugs into the STk evaluator:
(define switch (macro expr (macro-expand-switch expr)))
Instead we could define a macro, to take the symbolic derivative of an expression. So instead of writing
(let ((f complicated-expression-involving-x)
(df derivative-of-complicated-expression-involving-x-wrt-x))
... code using f and df ...)
we could define a macro, using the diff function from project one as a helper function, so that
this expands to the above:
(with-derivative f df complicated-expression-involving-x x ... code using f and df ...)Our macro is straightforward to write:
(define (with-derivative-expander expr)
(let ((f-var (cadr expr))
(df-var (caddr expr))
(complicated (cadddr expr))
(x-var (caddddr expr))
(body (cadddddr expr)))
`(let ((,f-var ,complicated)
(,df-var ,(diff complicated x-var)))
,body)))
If we wrote code like
(let ((key 154267))
(switch lock-type
((yale padlock) (foo key))
((deadbolt chain) (bar key))
((five-button combination) (baz key))))
then the key in (foo key) would not be 15267 but
rather the key bound by the code generated by the macro, ie
it would have the value of lock-type. Oops!
There are two ways to avoid this problem. One is to wrap code up in lambdas in a place outside the scope of the newly bound variable. The other is to use a variable name that no one else will ever use, thus avoiding any possibility of a collision. To do this, we can define a helper function that uses set! to make up a new symbol every time it's called, and then call it when we want to make up a new variable name.
(define gensym-counter 0) (define (gensym) (set! gensym-counter (+ gensym-counter 1)) (word 'gen_var_ gensym-counter))Now it will work like this
STk> (gensym) gen_var_1 STk> (gensym) gen_var_2 STk> (gensym) gen_var_3 STk> (list (gensym) (gensym)) (gen_var_4 gen_var_5)and we can rewrite our switch macro expander as follows:
(define (macro-expand-switch expr)
(let ((key-var (gensym)))
`(let ((,key-var ,(cadr expr)))
(cond ,@(map (lambda (clause) (expand-switch-clause key-var clause))
(cddr expr))))))
`(let ((,f-var ,complicated)
(,df-var ,(diff complicated x-var)))
,body)))
Without quasiquote this would be written
(list 'let
(list (list f-var complicated)
(list df-var (diff complicated x-var)))
body)
The `xxx is parsed (by the Scheme reader) as (quasiquote
xxx), and similarly ,xxx is parsed as (unquote
xxx) and ,@xxx as (unquote-splicing xxx). Then
the quasiquote macro takes over, and expands into the code
required to build the list specified.
Basically, quasiquote is just like regular quote, except that anything inside the quoted form preceded by a comma is evaluated, and anything preceded by a comma-at is evaluated and ``spliced in'', ie has its surrounding parenthesis removed.
Quasiquote is probably easier to figure out by example than by
explanation. Here is a table of equivalent code on the left and the
right.
| with quasiquote | without quasiquote | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
`foo | 'foo
| `,foo | foo
| `(a b c) | '(a b c)
| `(a ,b c) | (list 'a b 'c)
| `(a (aa ,b cc) c ,d) | (list 'a (list 'aa b 'cc) 'c d)
| `(,@foo) | foo
| `(a (aa ,@b cc) c ,d) | (list 'a (cons 'aa (append b '(cc))) 'c d)
| |
For more practice, try some Backquote Exercises.